프로그래머스 코딩테스트연습 Level3 정수삼각형 C++
by 진혀크
문제설명
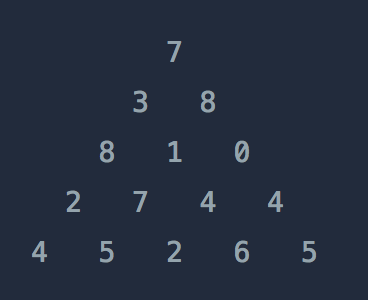 위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한 사항
- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
입출력 예제
triangle result
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30
접근
- 문제 분류 자체가 다이나믹 프로그램이라 DP로 접근했다.
내가 생각한 풀이
- 양쪽 끝에 있는 부분은 올 수 있는 값이 정해져있다. 그 외의 부분은 2가지 중 하나를 선택해야 하는데 코드를 참고하면 쉽게 이해 할 수 있을 것이다.
코드
#include <string>
#include <vector>
using namespace std;
int solution(vector<vector<int>> triangle) {
int answer = 0, dp[501][501] = {0, };
dp[0][0] = triangle[0][0];
for(int i = 0 ; i<triangle.size(); i++)
{
for(int j = 0; j<i+1; j++)
{
if(j == 0)
{
dp[i][j] = dp[i-1][j] + triangle[i][j];
}
else if(j == i)
{
dp[i][j] = dp[i-1][j-1] + triangle[i][j];
}
else{
dp[i][j] = max(dp[i-1][j-1] + triangle[i][j], dp[i-1][j] + triangle[i][j]);
}
}
}
for(int i = 0 ;i<triangle.size();i++){
if(dp[triangle.size() - 1][i] > answer) answer = dp[triangle.size() - 1][i];
}
return answer;
}
Subscribe via RSS