문제

  • 그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.

그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

입력

  • 입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V(1≤V≤20,000)와 간선의 개수 E(1≤E≤200,000)가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호가 빈 칸을 사이에 두고 주어진다.

출력

  • K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

예제

예제 입력
2
3 2
1 3
2 3
4 4
1 2
2 3
3 4
4 2

예제 출력
YES
NO

접근

  • 이분 그래프란?
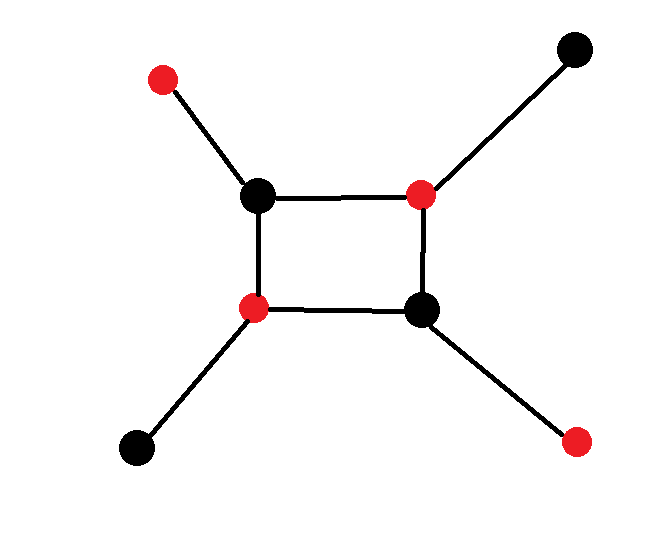
    • (투박한 그림 죄송합니다.) 위의 그림과 같이 각 노드를 색칠한다고 했을 때 모든 노드에 대해 인접한 노드와 자신의 노드의 색이 다르다면 이분 그래프라고 할 수 있다. 그래프가 떨어져 있어도 모든 노드가 다음 성질을 만족한다면 이분 그래프라고 할 수 있다.
  • 검색을 해보았더니 이분 그래프는 BFS를 통해 발견할 수 있다고 한다.
  • BFS를 통해 어떤 알고리즘을 짤 수 있을까?

내가 생각한 풀이

  • 우선 BFS를 통해 노드들의 색을 칠한다. 칠하는 도중 근접한 노드중 자신과 같은 색을 가진 노드가 있다면 break 시키고 NO를 출력한다.
  • 모든 색칠 작업이 끝난 후 각 노드를 돌며 주변에 같은 색상을 가진 노드가 있나 확인한다.
  • 정점이 20000개, 간선이 200000개라는 점을 고려하여 vector를 활용하기로 했다.

코드

#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int main(void){
  cin.tie(NULL);
  ios_base::sync_with_stdio(false);
  int c,V,E;
  cin>>c;
  for(int i = 0 ;i<c;i++){
    vector<int> v[20002]; //메모리 초과를 방지하기 위해 vector를 사용함.
    int chk[20002] = {0, }, clr[20002] = {0, }, r=0; //chk는 방문했는지 기록하는 배열, clr은 각 vertex의 색을 저장하기 위한 배열.
    queue<int> q;
    cin>>V>>E;
    for(int j = 0 ;j<E;j++){
      int from, to;
      cin>>from>>to;
      v[from].push_back(to);
      v[to].push_back(from);
    }
    for(int j = 1 ;j<=V;j++){ //그래프가 두 개 이상일 수 있으므로 모든 정점에 대해 검사를 실행한다.
      if(chk[j]==0){q.push(j);}
      while(!q.empty()){
        int t = q.front();
        q.pop();
        for(int j = 0 ;j<v[t].size();j++){
          if(chk[v[t][j]] == 0){ //처음 도달한 정점이라면 check를 해주고 이전과 다른 색으로 칠한다. 그 후 큐에 push한다.
            chk[v[t][j]] = 1;
            clr[v[t][j]] = (clr[t]+1)%2;
            q.push(v[t][j]);
          }
          else{
            if(clr[v[t][j]] == clr[t]){ //만약 한 번이라도 방문을 했다면 색을 검사한다. 이 때 색이 같다면 이분그래프가 아니므로 이분 그래프인지 아닌지 체크하는 r을 1로 바꿔준다.
              r = 1;
              break;
            }
          }
        }
      }
    }
    if(r==1){cout<<"NO"<<'\n'; continue;}
    else{//앞서 발견하지 못했을 수도 있는 반례를 찾기 위해 각 점을 돌아다니며 같은 색이 있는지 체크한다.
      for(int j = 1;j<=V;j++){
        for(int k = 0;k<v[j].size();k++){
          if(clr[v[j][k]] == clr[j]){
            r = 1;
            break;
          }
        }
      }
    }
    if(r==1) cout<<"NO"<<'\n';
    else cout<<"YES"<<'\n';
  }
  return 0;
}